L. David Roper
http://www.roperld.com/personal/roperldavid.htm
I have also done a detailed calculation of global warming due to fossil-fuels burning.
The purpose of this article is to show the energy deficit in future years by extrapolating world energy consumption and coal, crude-oil, natural-gas and uranium extraction into future years.
A calculation of energy produced by nuclear reactors is shown to be rather small compared to the projected energy consumption and the energy available from the three fossil fuels. Therefore, the only way to fill the energy deficit beyond fossil-fuels energy is by renewable energy, such as solar and wind.
It is then shown that a reasonable growth rate for three renewable energy sources (wind, photovoltaics and biofuels) can meet an assumed asymptotic energy per capita of 350x106 BTU/year/person.
"Energy" here refers to the total energy available in the fuel, often called "primary energy", not the energy actually converted into useful work or electricity.
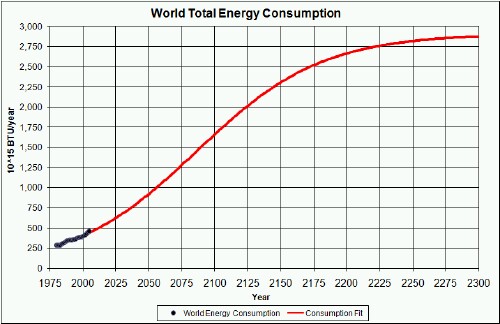
Of course, energy consumption by humans cannot grow indefinitely, because there is a limit to the amount of energy that can be captured from the Sun. The graph below shows the world energy-consumption data and a hyperbolic-tangent-function fit to the data in order to extrapolate into the future with an eventual asymptotic consumption amount of 350x106 BTU/year/person (~12 kW/person), for an assumed final asymptotic population of about 8.3x109. This is about the per-capita consumption of the United States now. This amounts to a consumption asymptote of about 2900x1015 BTU/year [2900 quad/year or (2900*1055)x1015 joules/year=3.06x1021 J/yr=9.69x1010 kilowatts=8.50x1014 kWh/year]:

Currently the U.S. uses about 350x106 BTU/person/year (~12 kW/person), industrialized countries average about 200x106 BTU/person/year (~6.5 kW/person), developing countries average about 35x106 BTU/person/year (~1.2 kW/person) and the world average is about 75x106 BTU/person/year (~2.5 kW/person). The leveling off assumes that renewable energy sources will be developed in time to make the transition from the peaked fossil-fuels extraction curve to the smoothly rising energy-consumption curve.
The main sources of energy for the world are coal, crude oil and natural gas. The following constants are needed to calculate the amount of energy that can be obtained from these three fossil fuels:
The graph below shows the energy obtainable from fossil fuels as a function of time, using these constants and the depletion curves of coal, crude oil and natural gas and assuming that 75% of fossil-fuels extraction amount is burned for energy in the year they are extracted:
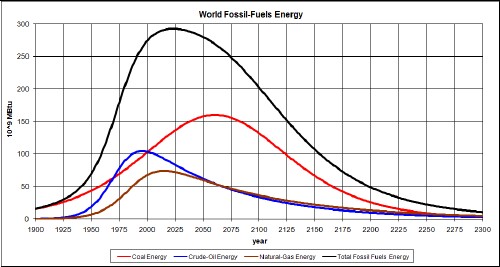
(The 75% assumption is a rough approximation. Surely, each fossil fuel has a different fraction that is burned for energy and the fractions undoubtedly vary with time.)
The graph below compares the world energy consumption to the total energy supplied by fossil fuels:
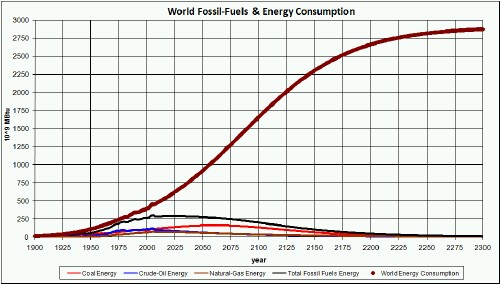
As should be the case, other energy sources besides fossil fuels supply some of the energy consumption. There is a huge energy deficit relative to fossil-fuels energy to meet the 350 MBTU/person/year asymptote.
An interesting next question to ask is how much primary energy is supplied by "burning" uranium in nuclear reactors? The best analysis of energy produced by nuclear reactors I have found gives the following constants needed to do this calculation:
The amount of nuclear thermal energy produced by reactors as a function of time, assuming a very optimistic amount of nuclear resources, is shown in the following graph:
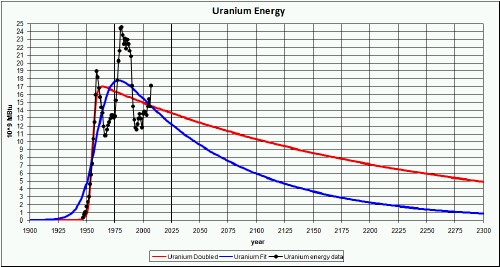
The red curve is a fit where the amount to eventually be extracted is double the amount of the blue curve, an extremely optimistic case.
It was assumed that all uranium mined is eventually used to extract energy. Of course, much of it was used and will be used to make nuclear weapons; however, some weapons were dismantled and their uranium used to extract energy. So this calculation is extremely optimistic for useful electrical energy that can be gotten from uranium.
The graph below compares the world energy consumption to the total energy supplied by the fossil fuels and uranium:
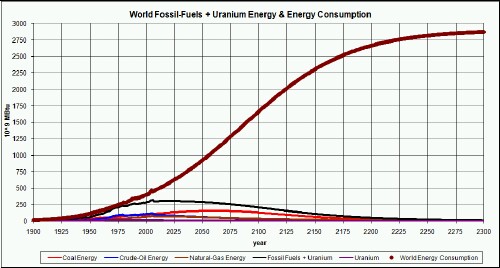
Doubling the total uranium finally extracted has very little effect. The conclusion is that uranium will never supply very much energy for humans to use.
The amount of energy that must be supplied by sources other than fossil fuels and uranium are shown in the graph below:
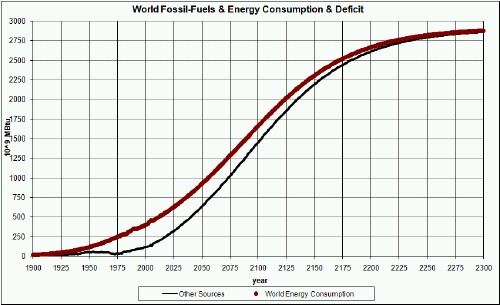
It is possible that the decline in extraction of fossil fuels will cause a population collapse. This would surely cause the world energy consumption to also fall to some new asymptote. In that case the amount of energy that must be supplied by other than fossil fuels and uranium would be less than shown above.
The growth rates for renewable sources have been as follows at the beginning of the 22nd century:
In recent years renewable energy has supplied about 14% of primary energy consumed.
Roughly assume that wind supplies one-half of renewable energy, photovoltaics supplies one-fourth and biofuels (biodiesel and ethanol) supplies one-fourth. A hyperbolic-tangent function is used to represent their growth and their eventually reaching an "asymptote" below the other-sources curve as they were about year 2000. For a hyperbolic-tangent time constant of 20 years and a break-point year of 2015, the result is shown in the graph below:
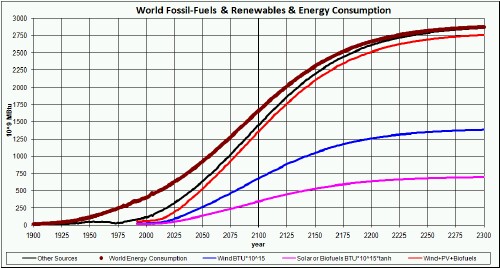
The renewable-energy growth rates versus time are:
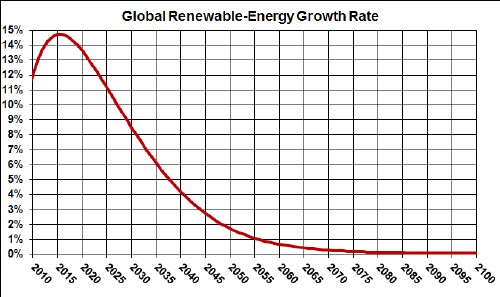
The peak is about twice the 2015 growth rate of ~7.5%. These are achievable growth rates, but will require a massive effort for about 1.5 decades.
An interesting further study would be to calculate how much of the Earth's surface is required to meet these values for energy from photovoltaics and biofuels and whether sufficient wind resources are available to meet these values for wind energy. Possibly the best biofuel is biodiesel and the best source of feedstock for biodiesel is algae.
For a rough calculation, consider that the Sun shines about 5 kWh/m2/day (1.8x107 J/m2/day or 1.7x104 BTU/m2/day) on the Earth surface. For a Earth land area of about 1.5x1014 m2, the total solar energy on the land area is about 9.3x1020 BTU/year. The asymptotic energy consumption used above is about 3x1018 BTU/year. So the available solar energy shining on the land is about 310 times that amount that is assumed to be consumed. This implies that the assumed asymptotic consumption is probably higher than possible. Of course, the ocean area is much larger than the land area (71% compared to 21%), so some of the energy could come from the solar energy impinging on the oceans.
The conclusion is that, if the world could level off energy consumption to about 575 quad per year, a continued intensive program of increasing renewable energy sources at a reasonable rate could easily meet the energy needs not met by fossil fuels and uranium.
The depletion of fossil fuels (coal, crude oil and natural gas) indicate that the time is now for beginning a world intensive program to develop renewable fuel sources (wind, solar and biofuels). In fact, the current rates of growth of renewable-energy sources are more than enough to match the growth in energy consumption and then slow down in growth to make up the difference between the decline of biofuels and a reasonable final per capita use of energy (350x106 BTU/year/person).
Because of depletion, uranium will never be able to supply much energy compared to the need. Precious fossil fuels should be used to develop renewable energy sources rather than more nuclear reactors.
Further study needs to be done as to whether the proposed continued growth of renewable-energy sources is possible on a finite Earth.
I believe that humans will continue to extract and burn fossil-fuels as fast as possible. Fortunately, the peaking of fossil-fuels extraction will put a natural brake on that burning. Unfortunately, the peaking of fossil-fuels extraction will cause massive disruptions in meeting the sustenance needs of nearly 7 billion humans. Also, the increase in temperature in about the year 2100 of about 1.4°C (2.5°F) above the 19th-century temperature will cause great suffering. The current emphasis on cutting back carbon emissions from fossil-fuels burning is needed to reduce global warming, but even more to preserve the fossil fuels for making useful materials and to prepare society for the economic disruptions that will undoubtedly occur when the populace finally realizes that we are on the down side of fossil-fuels depletion.
Probably the best that we can corporately do is to plan for the disruptions that will occur, both from the increase in temperature until 2100, and possibly on into the future if methane clathrates come into play, and the decline of availability of fossil fuels. However, we should strenuously try to use fossil carbon compounds for useful materials instead of burning it for energy.
See a rough estimate of the carry capacity of the Earth after fossil fuels are burned up.
I have also done a detailed calculation of global warming due to fossil-fuels burning.
The asymmetric peaked Verhulst function is used to fit the fossil-fuels extraction data:
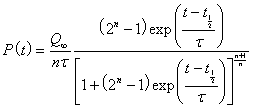
where 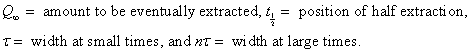
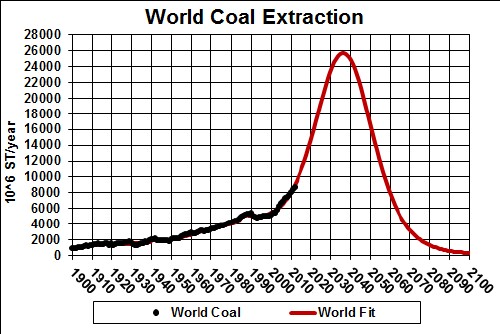
The total amount to be extracted (area under the curve) is 1.3 x 1012 tons.
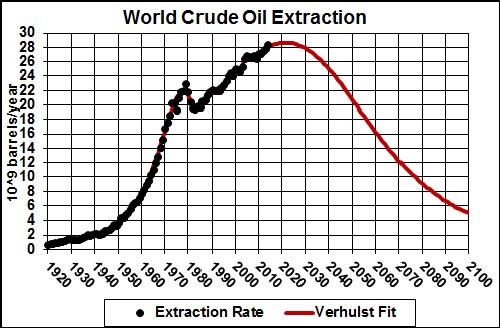
The total amount to be extracted (area under the curve) is 3 x 1012 barrels.
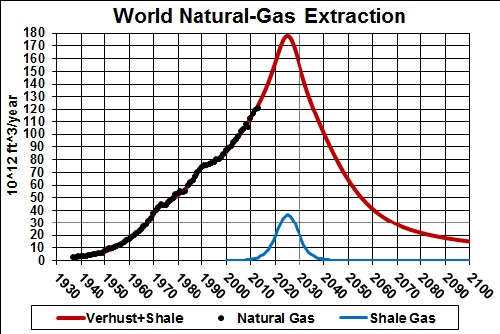
The total amount to be extracted (area under the curve) is 13.5 x 1015 ft 3 = 13.5 x 1012 mcf.
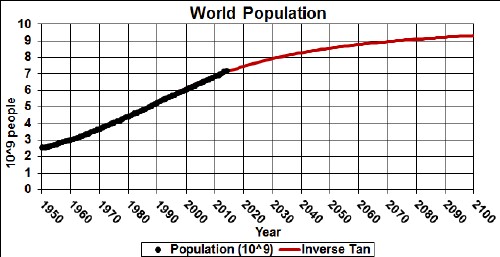
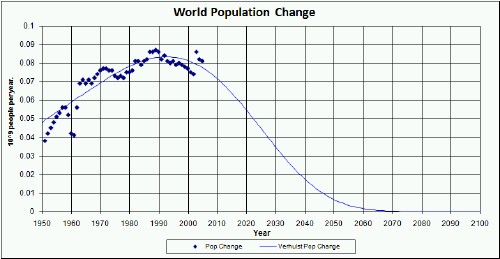
The bottom graph shows the change in population, with a peak at about 1990-95.
One can make a good case that world population is proportional to the availability of fossil-fuels energy. I have fitted world population from 1950 to 2006 to available fossil-fuels energy and projected it into the future:
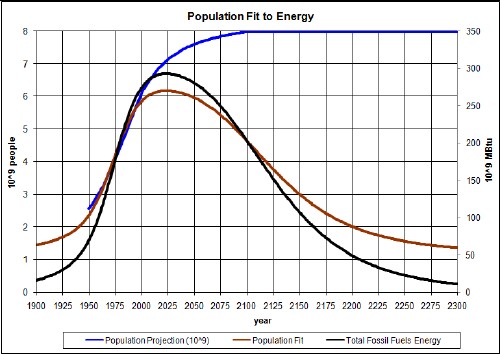
The blue curve projects world population to a final asymptote of 8 x 109 people, which can only happen if renewable energy is highly developed.. The brown curve is the world population projection for the fit to available fossil-fuels energy, which would likely be the case if renewable energy is not used.. I would guess that a population decline is likely, but perhaps not as severe as the brown curve.
20-Nov-2016