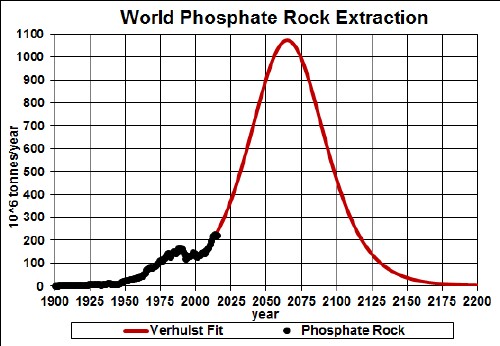
Phosphate-rock extraction rate for the world and a Verhulst functions fit to the data.
L. David Roper
http://www.roperld.com/personal/RoperLDavid.htm
2 July, 2016
Phosphate rock is indispensible in creating fertilizer for modern farming. It is also used in modern batteries. The graph below shows the phosphate-rock extraction data for the world and a Verhulst functions fit to the data in order to extrapolate into the future.

Phosphate-rock extraction rate for the world and a Verhulst functions fit to the data.
The red curve is a fit with total amount to be extracted of ~75x109 tonnes, which incorporates the latest reserves estimate (~67x109 tonnes).
For more information about phosphate rock:
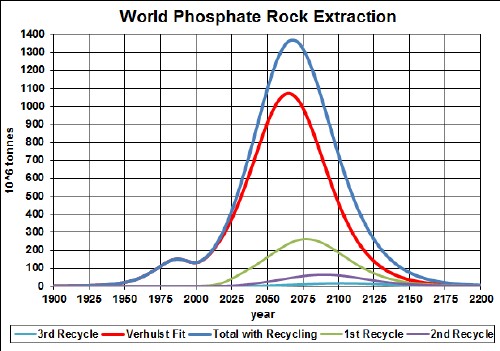
Phosphate has not been recycled, but efforts are underway to recycle it from sewage. It is being used in batteries now, so that phosphate will probably be recycled. Assume that:
The effective phosphate rock available for use after the first ten recycling cycles is shown in the following graph, along with the effective phosphate rock available for each cycle:
The equation for a recyling cycle is
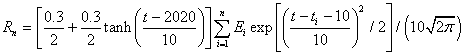 ,
,
where Ei is the amount available from the previous cycle. Here is an example of the Excel coding:
{=(($J$2+$I$2)/2+(($J$2-$I$2)/2)*TANH((A27-$K$2)/$L$2))*SUM($I$27:I27*(EXP(-1*((A27-$A$27:A27-$N$2)/$O$2)^2/2))/$O$2/SQRT(2*PI()))} (The curly bracket surrounding the term makes it into an array; it must be entered by holding down the SHIFT & CTRL keys while pressing the ENTER key.)
Of course, the recycling could be extended to more cycles, skewing the curve further into the future. However, the peak and fall off after it will not change because further cycles are essentally zero in that time region.
Thus, under the assumptions given above, the effective amount of phosphate rock available for making items peaks at about 2035 and falls off rapidly after that. Humans will have taken concentrated phosphate-rock deposits and scattered them across the surface of the earth.
The Excel spreadsheet is set up to make it easy to calculate with different recycling assumptions.
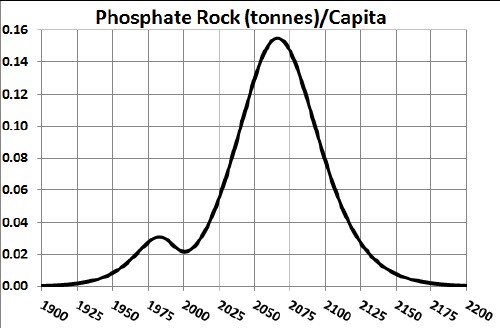
Dividing the recycling curve above by the projected world population (asymptote ~1010), one gets: