Physics of the 2005 Toyota Prius

The 2004/2005 model of the Toyota Prius automobile is a parallel/series full hybrid without a standard transmission. Instead, a small set of planetary gears, called a "Power Split Device" (PSD) serves as the mechanism for driving the wheels of the vehicle in a manner that simulates a continuously variable transmission. Complex electronic controls manage the PDS, so it is called an Electronic Continuously Variable Transmission (ECVT).

This is the arrangement of the Power Split Device gears.
(Taken from The Power Split Device by Graham Davies.)


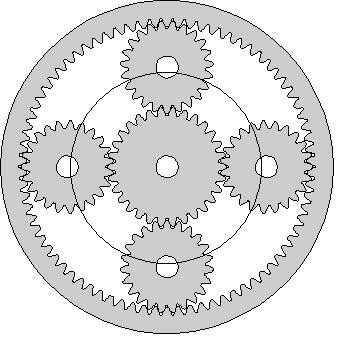
The diameter is about the height of a soft-drink can.
The outer gear with 78 inward teeth is called the "Ring" gear. The center gear with 30 teeth is called the "Sun" gear. The four middle "Planet" gears' shafts are attached to a circular "Planet Carrier" that can rotate around the same axis as the Sun gear. The number of teeth in the planet gears is not important. The ring gear also has teeth on the outside which drive a steel chain that leads to reduction gears and the front-axle differential.
As shown in the diagram below the Planet Carrier is attached to the gasoline engine shaft, the Sun gear is attached to the smaller electric generator/motor (SGM = MG1) and the Ring gear is attached to the larger electric motor/generator (LMG = MG2) and the vehicle's wheels through some reduction gears and a standard differential.
(Taken from PowertTrain Components by Graham Davies.)
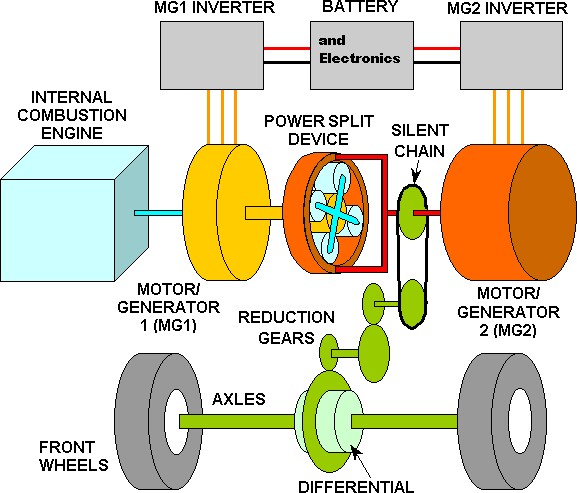A drawing of how the engine and motors system is laid out (from http://www.ornl.gov/~webworks/cppr/y2001/rpt/122586.pdf):

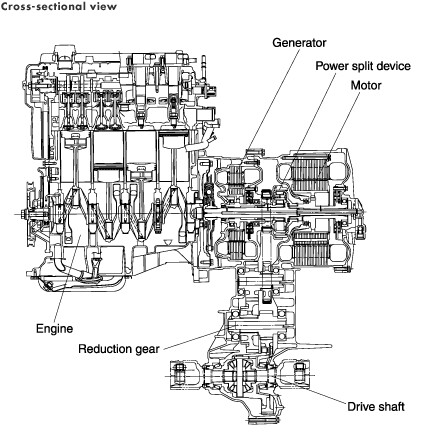
"Generator" refers to the smaller generator/motor (MG1 = SGM); "Motor" refers to the larger motor/generator (MG2 = LMG).
Toyota Prius Specifications
  • Engine: 1.497 cc, 76 hp (57 kW) @ 5000 rpm, compression ratio 13.0/1, Atkinson cycle
  • Motor/generator: 500 V Permanent Magnet rotor AC Sync, 67 hp (50 kW) @ 1200-1540 rpm
  • Generator/motor: 500 V PM AC Sync, 17 hp (13 kW). Starts engine at 1000 rpm when needed. Can turn up to 10,000 rpm.
  • Traction Battery: 201.6 V Ni-MH, 21 kW (28 hp)
  • Net Hybrid System power: 110 hp (82 kW)
  • Heated coolant before starting engine
  • Regenerative coasting and braking
  • Realistic Mileage: 40-50 mpg (EPA: 51-60 not so)
  • 90% less emmisions than other new cars.

Many more details about the mechanics and electronics of the 2005 Prius are available at:

The first of the above links gives a graph of power measurments for different vehicle speeds:


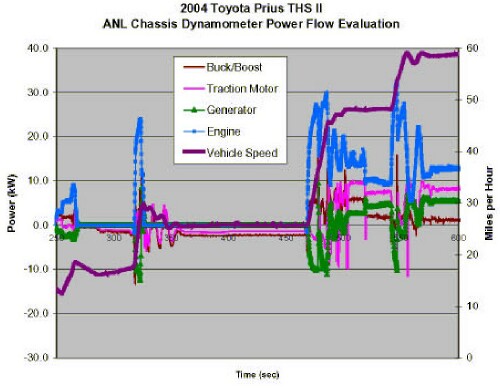
Buck/Boost = power from the 201 volt battery being boosted to 500 V to run LMG or bucked from 500 V to 201 V (negative power) to charge the battery. Note how it closely matches the LMG power. Traction Motor = LMG. Generator = SGM. Vehicle speed is given on the right scale.
  • Starting from the left, the speed is about 12 mph and the generator (negative power for SGM) starts the engine.
  • The car accelerates to about 19 mph and then deccelerates a little; then the engine turns off. The LMG turns into a generator to charge the battery.
  • Then the car accelerates to about 30 mph. The SGM starts the engine again and a large peak of engine power does most of the work, with help from LMG. Note that LMG oscillates between providing motive power and charging the battery (negative power) after the acceleration.
  • The car speed slows to about 26 mph with the engine off and the LMG charging the battery slightly.
  • Then the car accelerates to about 48 mph. The engine is started by SGM and provides the power for the acceleration. Note the power oscillation for LGM again and a complementary oscillation of the engine power. The SMG also oscillates between being a generator to send power to LGM or charge the battery and being a motor to power the wheels.
  • At the steady speed of about 48 mph the engine provides about 10 kW, the LMG provides about 8 kW and the SGM provides about 4 kW to power the motion of the car.
  • Then the car accelerates again to about 59 mph. SGM becomes a generator to provide power to LMG, which shows a short burst of power. Again oscillations occur.
  • Finally, at a steady speed of about 59 mph the engine power is about 12 kW, the LMG power is about 9 kW and the SGM power as a motor is about 5 kW. The battery (Buck/Boost) power is about 1 kW, so the
Measurements made in France regarding the power situation for SGM and LMG:
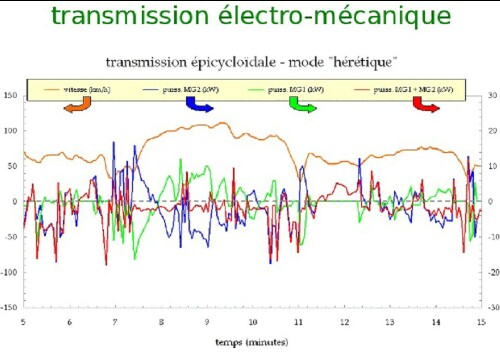Note that SGM=MG1 and LMG=MG2 alternate between being motors and generators, with a net generation to charge the battery. (Vitesse = speed, Puiss. = power)

Graham Davies has determined many of the mechanic parameters and operating procedures of the 2004/2005 Toyota Prius' power train. The following table lists some of the important facts that are necessary to study the physics of the operation of the Pruis.

Let:

  • S = angular velocity (rpm) of the Sun (inner) gear that connects to the Smaller electric generator/motor (SGM = MG1) It is a generator providing power to the larger motor/generator or to the battery, except when it is needed as a motor to start the gasoline engine. Sometimes it acts as a motor to power the wheels.
  • L = angular velocity (rpm) of the Ring (outer) gear that connects to the Larger electric motor/generator (LMG = MG2) and to the reduction gears to the vehicle's wheels. It is configured as a motor when it is need to provide motive power and is configured as a generator when it is needed to charge the battery.
  • E = angular velocity (rpm) of the Planet Carrier, and thus the Engine shaft.
  • V = speed (mph) of the vehicle. Davies calculated that L = 59.2*V for the 2001-3 Prius; however for the 2004-2005 Prius it is L = 60.1 V .
Davies showed that the equation that connects these variables is:
S = (1 + 78/30) E - (78/30) L = (1 + 78/30) E - (78/30) 60.1 Vand that the engine torque (Et) passed to the sun gear is St = [30/(30+78)] Et and the engine torque passed to the ring gear is Lt = [78/(30+78)] Et.
Another way to think of the PSD is as an asymmetrical differential. For a differential the number of teeth is the same for the two sides of the differential that feed power to the two wheels.
Then the equation is S = (1 + n/n) R - (n/n) L = 2 R - L or 2 R = S + L, where n = number of teeth in both gears. The Pruis has such a standard differential located below the engine-motors complex.

An arbitrary example that probably does not fit the system power parameters, but may be a reasonable first approximation:

  • Let V = 60 tanh(t/5); i.e., the speed of the vehicle smoothly goes from 0 at 0 seconds to 60 mph at 10 seconds.
  • Let E = 500 + 6000[1 + tanh({t-5}/5)]/2 - 5000[1 + tanh({t-10}/2)]/2; i.e., the engine rpm smoothly goes from about 1200 rpm to about 4500 rpm and then settles down to about 1500 rpm.
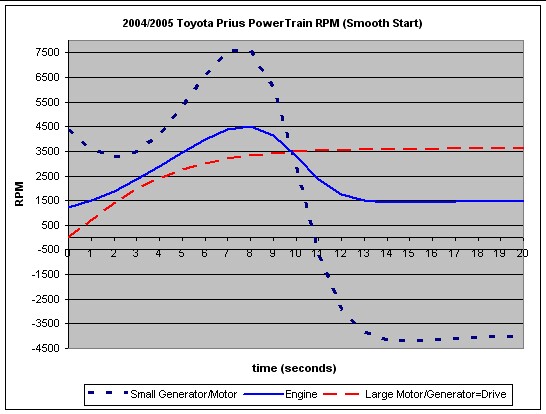Note that the SGM has to speed up in order that the engine can have a high rpm and that the vehicle can smoothly approach the final speed. In this case the SGM is electronically configured as a generator and passes the power it generates on to the LMG to supplement electric power from the battery. Both the LMG and the engine provide the power needed to accelerate. At the final speed, the LMG is electronically configured as a motor to supplement the power of the engine or as a generator to charge the battery. At higher speeds the SGM is electronically configured as a motor to help power the vehicle or as a generator to feed power to LMG. The peak torque of the engine and the motor occur around 4200 rpm and 0-1200 rpm, respectively, just at the right time to cause the vehicle's acceleration. Some of the power the LMG uses for the acceleration comes from the SGM. This model does not account for the alternation between LMG and SGM as generators and motor, as shown in the actual measurements given above.
The following Power-Split-Device simulations are taken from http://home.earthlink.net/~graham1/MyToyotaPrius/Understanding/WhatsGoingOnAsIDrive.htm:

Moving in reverse:

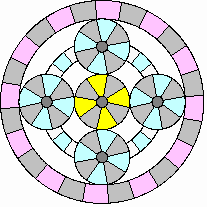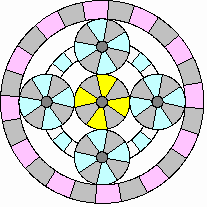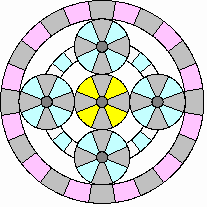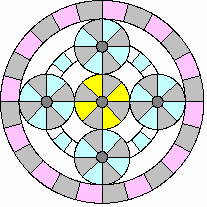Starting engine at rest:

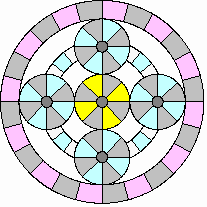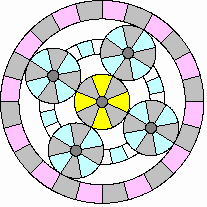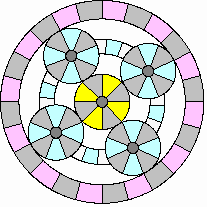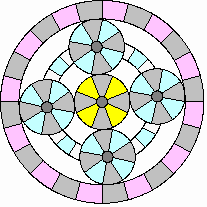Accelerating and hill climbing:

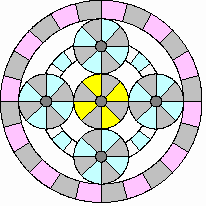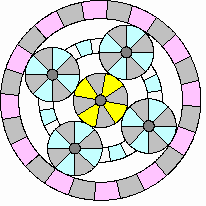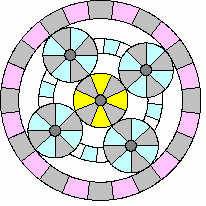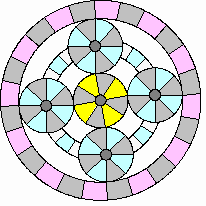Cruising:

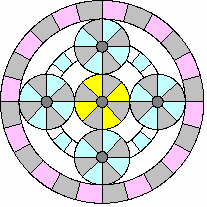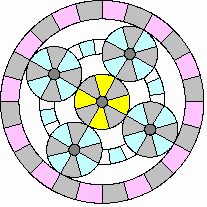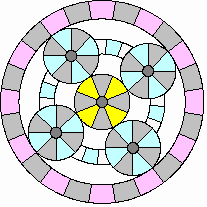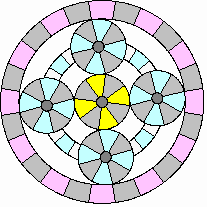
Coasting, braking and slow driving (< 25 mph)
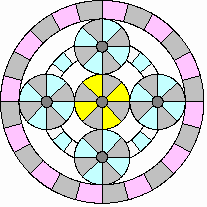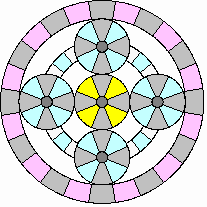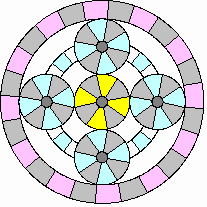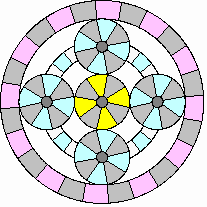All together:
Moving in reverse:
 Starting engine at rest:
Accelerating and hill climbing:
 Cruising:
Coasting, braking andslow driving (< 25 mph):

Taken from a Toyota document.
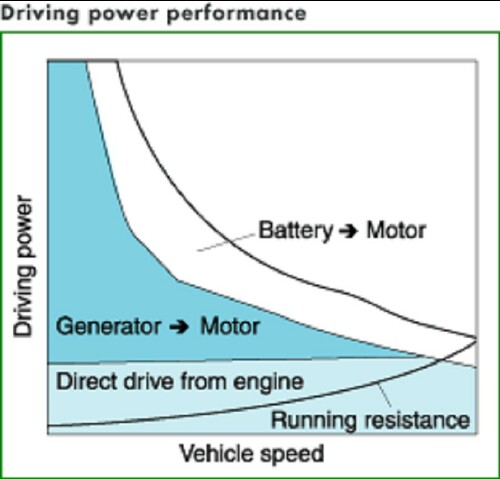
Note:
  • At very low speeds most of the power is supplied by the LMG.
  • If the engine is running most of the power for LMG comes from SGM by means of the engine driving it.
  • As speed increases the engine provides increasingly more of the power.
  • At medium speed the LMG and engine approximately equally share in providing power to the vehicle.
  • At high speed most of the power comes from the engine.
Below is an attempt to mathematically model the bahaviour of the Prius power system. To do so mathematical expressions are needed for the engine and LMG power and torque:
Engine power versus rpm:
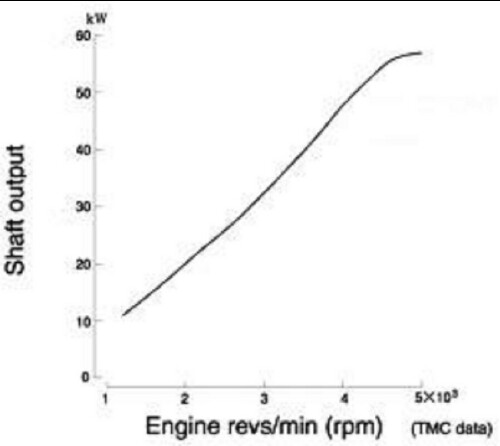An equation that fits the above curve fairly well is Ep = 57 [1 + tanh({rpm - 2500}/2000)]/2 .
See below for the fit.
Engine torque versus rpm:
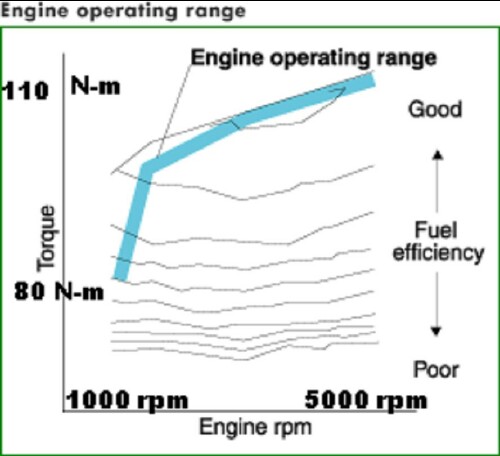An equation that fits the above curve fairly well is Et = 109 tanh(rpm/1097) .
See below for the fit
Motor power versus rpm:
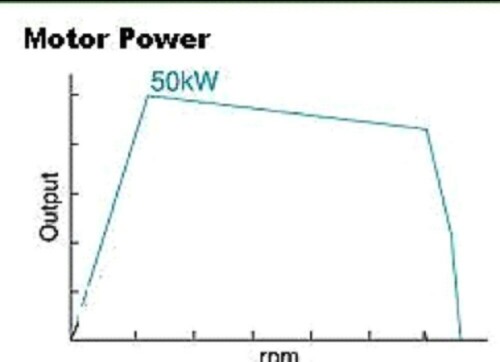An equation that fits the above curve fairly well is
Mp = 50 [1+tanh({rpm-600}/200)]/2-5 [1+tanh({rpm-3500}/2000)]/2-45 [1+tanh({rpm-6500}/100)]/2 .
See below for the fit.
Motor torque versus rpm:
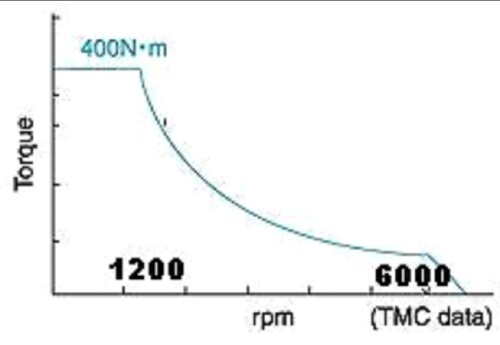An exponential equation that fits the above curve fairly well is
Mt = 85.39 + 10.38 exp[(rpm - 4369)/1137].
See below for the fit.
The following curve shows the fits of the equations given above to the engine and motor power curves:
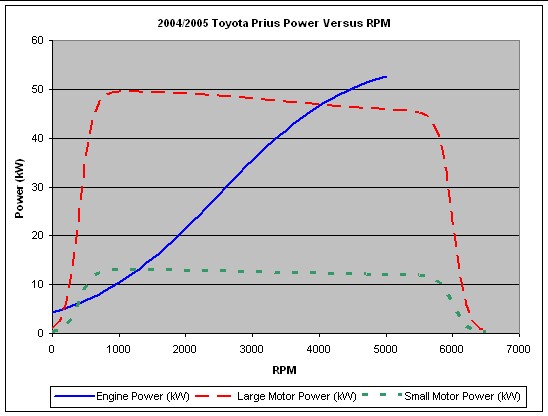The following curve shows the fit of the equation given above to the engine torque curve:
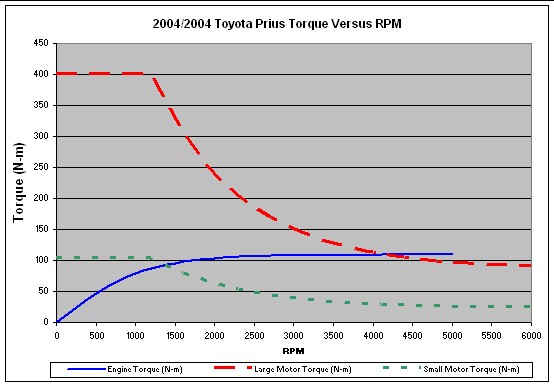When the LMG is being used as a motor, the engine p ower curve given above can be used to calculate its contribution to the power sent to the wheels. A similar curve is needed for the SGM when it is being used as a motor; perhaps the same curve scaled down to the relative power of SGM is applicable. When LMG or SGM are being used as generators, the power generated by them is calculated by multiplying the torque supplied to them by their rpm.
Now we combine the example given above with the engine and motor power curves and the SGM power calculated by multiplying the appropriate fraction of the engine torque times the SGM rpm:

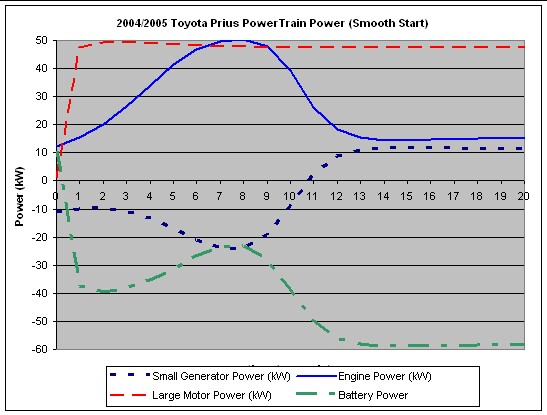
Note that SGM is a generator (negative power) that supplies power to the LMG, along with the battery. Once the rpms are high, the LMG provides almost constant power. At some point these curves do not apply because maintaining a constant speed does not require much power; so the motor becomes a generator to charge the battery. In fact, as the measured data given above shows, SGM and LMG alternate between being generators and motors, with a net generation to charge the battery.

Modes of Operation of E, S and L

The engine E can have the following modes of operation:

The small generator/motor SGM or S can have the following modes of operation:

The large motor/generator LMG or L can have the following mode of operation:

Power On

When the driver pushes on the foot brake pedal and presses the finger Power button, the vehicle's electrical systems are started, making the accelerator foot pedal active.

Reverse Motion

Assume that the first motion is to back out of a garage. The hand shift lever is pushed left and up to engage the electric reverse-motion mode. The driver has seven seconds to back the vehicle out of the garage before the gasoline engine starts to warm up itself and the catalytic converter.

First consider what happens in the first seven seconds. The engine is immobilized with all 12 valves in the 4 cylinders closed, so that air compression in the cylinders prevents the engine shaft from rotating. That is, E = 0 and S = -(78/30) L . Assume that the vehicle goes from V = 0 to V = -5 mph in about 2 seconds according to the equation V(t) = -5 tanh(t)mph .

Then L(t) = -60.1 [5 tanh(t)] rpm and S(t) = (78/30)(60.1)[5 tanh(t)] rpm . Although L < 0, the electronics is arranged such that LMG acts as a motor to back up the vehicle. The SGM spins freely with no electrical connection to the battery or LMG. P:lots of L(t) and S(t) are shown below:

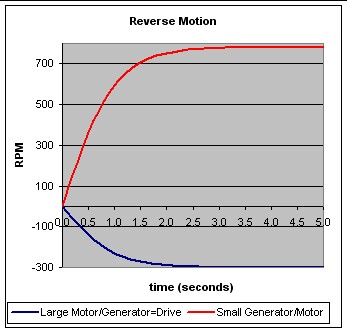
Starting the Engine

Now, assume that the foot accelerator pedal is not pushed within seven seconds after the finger Power button is pushed. The vehicle is not moving (L = 0 and V = 0). The electronics causes the SGM to be powered by the battery to start the engine at about 1000 rpm. Thus, S = (108/30) E = (108/30) 1000 rpm = .3600 rpm

Now, consider the situation that the engine starts while the vehicle is backing up at 5 mph. Then V = -5 mph, L = -60.1 (5) rpm, E = 1000 rpm. Therefore, S = (108/30)(1000) - (78/30)(-60.1 (5)) = 4381 rpm = S. SGM has to spin faster because the vehicle is moving backward.

Of course, the engines valves are opened in the proper sequences, fuel injection occurs at the proper times and firing occurs at the proper times tostart the engine. (Actually, one two cylinders are fired initially.)

Now consider the situation in which the engine starts while the vehicle is moving forward at, say 20 mph:

V = 20 mph, L = 60.1 (20) = 1202 rpm, E = 1000 rpm.

Then S = (108/30)(1000) -(78/30)(1202) = 475 rpm = S

The SGM does not have to provide much power to start the engine because the forward motion of the vehicle supplies most of the power.

The vehicle speed below which the SGM must act as a motor to help start the engine is given by setting S = 0:

0 = (108/30)(1000) - (78/30) 60.1 V or V = [108(1000)]/[78 (60.1)] = 23 mph = V.

Above this speed the engine starts by just using the forward motion of the vehicle. Just opening the valves, injecting fuel and firing starts the engine. The SGM either spins freely unconnected to the electrical system or it serves as a parallel motor with the LMG to drive the car or it serves as a generator to provide power to LMG or the battery. Perhaps this is the reason that the Pruis can be driven electrically up to about 24 mph without the use of the engine.

Regenerative Deceleration or Braking

Consider the situation where the driver's foot is lifted from the accelerator pedal such that slow deceleration occurs. The engine stops, so E = 0. Then the SGM and/or the LMG are electrically connected to the battery such that electrons flow toward the battery to charge it. The power used for this is taken from the motion of the vehicle.

Now consider the situation where the driver's foot is then used to press on the brake pedal. This causes the electrical system to reduce the resistance of the circuit to the battery so that the current is increased. This causes more power to be removed from the motion of the car. The amount of power that is removed from the motion is determined by the force the foot exerts on the brake pedal.

As an example let V(t) = 30 [1 - tanh(t/30)] for braking from 60 mph to a stop.

Then L(t) = 60.1 V(t) and S(t) = - (78/30)(60.1) V(t). P:lots of L(t) and S(t) are shown below:

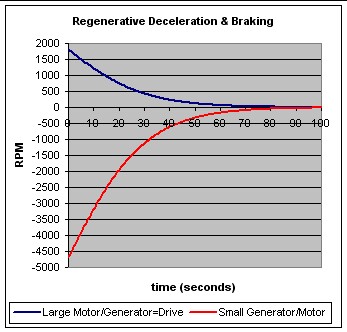
Accelerating to Cruising

Consider the case in which the vehicle is accelerated from rest with the engine just started.

Then using S = (1 + 78/30) E - (78/30) 60.1 V, one gets the following plot:

The SGM is initially deployed as a generator to provide power to the LMG to help the engine accelerate the vehicle. After the final speed is reached it may be deployed as a motor to help drive the vehicle or as a generator to charge the battery. Note that SGM spins backward after the final speed is reached.

Engine Braking

If the driver's foot tires of pushing on the brake pedal going down a long hill, the B position on the motion selector lever can be set to B to actuate engine braking instead of or in addition to regenerative braking by normal deceleration or braking.

Apparently for this case some valves are opened in the engine's cylinders to allow the engine to rotate its shaft (E > 0) and move its cylinders. No fuel is injected, so the engine does not provide any power; instead it absorbs power by compression of air and friction. Then S = (108/30) E - (78/30)(60.1) V. S and E can take on various combinations of values that satisfy this equation for a given V. E could be set at some safe value (say 1500 rpm) by varying the time intervals that the valves are opened. The LMG is electronically configured to be a generator to recharge the battery. The SGM could alo be configured to be a generator, but it may just spin freely.

L. David Roper, roperld@vt.edu