Mutual-Positive-Feedback Mathematics
L. David Roper
http://www.roperld.com/personal/roperldavid.htm
6 April, 2016
Introduction
There are many physical situations where two or more variables mutually interact to create positive feedback. An example is Earth average temperature and carbon-dioxide concentration in the atmosphere.
This article devises a simple model to account for positive feedback between two variables.
Consider two variables, A and B, that mutually interact to create positive feedback. Assume that the feedback time dependence is governed by the hyperbolic tangent function, tanh (x). (See http://www.roperld.com/science/hyperbolictangentworld.pdf). That is, there is a time delay for one variable to react to the change in the other variable in the same direction; the time delay may be different for each of the two variables.
The following form will be used to incorporate the hyperbolic tangent function in the feedback mechanism:
.
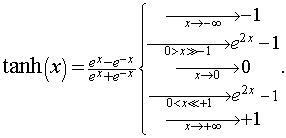
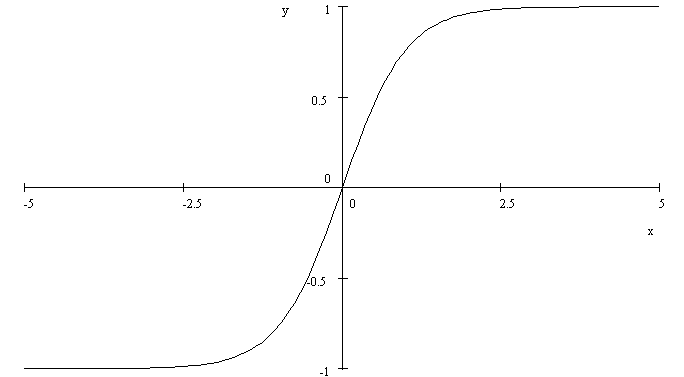
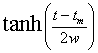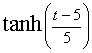is:
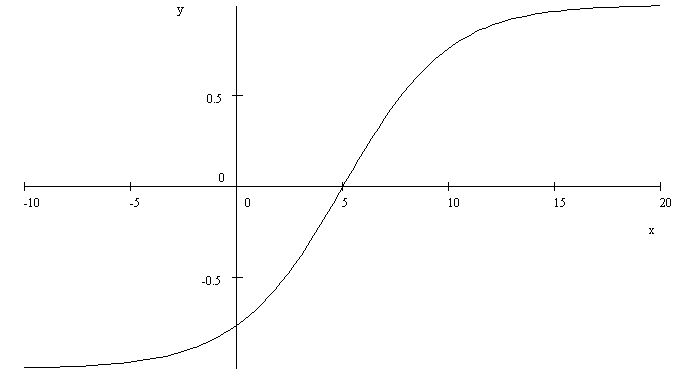
Sometimes the hyperbolic tangent is needed to start from 0 instead of -1 (zero-start hyperbolic tangent):
.
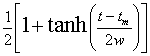Model for Mutual-Positive Feedback between Two Variables
The model used here for mutual-positive feedback between two variables is an iterative one that converges very rapidly.
For the simplest realistic case, consider that variable A changes slowly from some steady-state value to a new steady-state value, arbitrarily set to zero, by the hyperbolic tangent from its midpoint (value 0). Then assume that, to a first-order approximation, variable B changes gradually from arbitrary value zero to some new value by the zero-start hyperbolic tangent. To a first-order approximation:
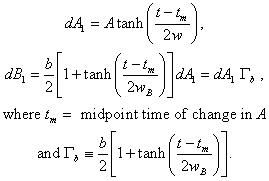
Similarly, when B changes as above in first order, A then changes gradually by the zero-start hyperbolic tangent to some new value. So, the second-order approximation is:
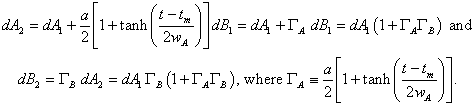
The third-order approximation is:
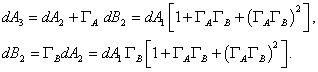
The fourth-order approximation is:
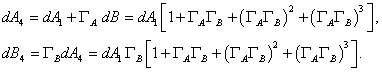
The nth-order approximation is:
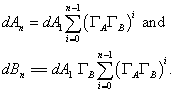
The result would be when 
However, the series may converge for just a few terms because of the asymptotic behavior of the hyperbolic tangent.
Example of the Model
Consider the simple case in which the mutual interaction is symmetrical:
That is, the time delay is the same for B when A changes as it is for A when B changes (parameters 
) and the amount of change is the same for both A and B (parameters 
).
The first four approximations are show in this graph:
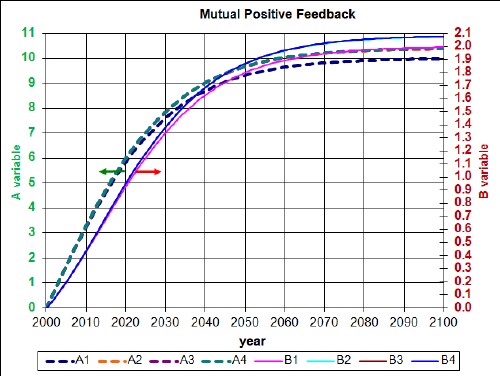
For this symmetric model highly accurate convergence occurs at the 3rd approximation and the result is quite good in the 2nd approximation. Even the 1st approximation is a good estimate for variable B.
A correlation calculation for the 4th approximation gives the correlations:
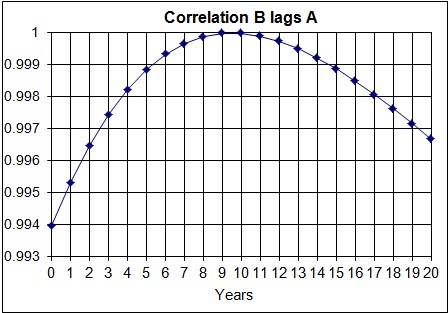
So, B lags A by about 9.5 years, because A was changed first. If B were changed first, A would lag B by the same number of years for a symmetrical mutual interaction. Therefore, two variables that mutually interact symmetrically to give mutual-positive feedback will lead or lag each other by the same number of time units depending on which one is changed first after a steady state situation.
Mutual-Positive-Feedback Model for Three Variables
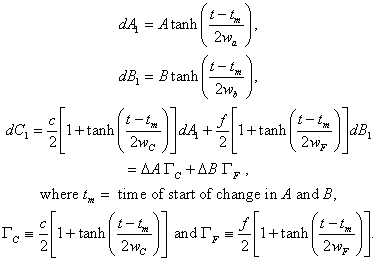
The second-order approximation is:
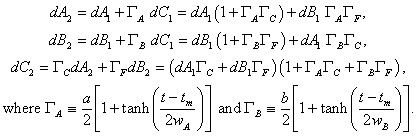
The third-order approximation is:
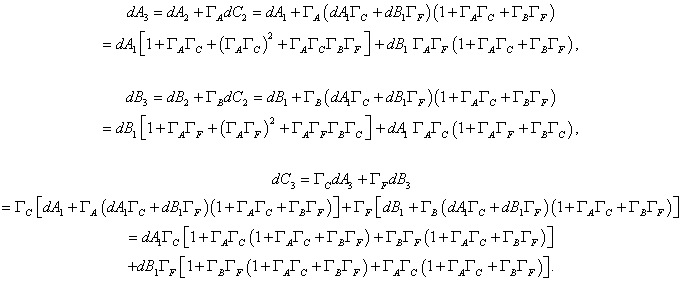
Conclusion
The mutual-positive-feedback model used in this work shows that which of two such interacting variables leads the other depends on which one was changed by interaction with some other variable.
Roper Global-Heating Web Pages
L. David Roper interdisciplinary studies