Human Intelligence Evolution

L. David Roper
http://www.roperld.com/personal/roperldavid.htm
6 April, 2016

Introduction

There is no agreed upon measure of human intelligence. One measure that has been proposed is the brain-to-body mass ratio, called the encephalization quotient (EQ) . In this article I collect the rough estimates for EQ for the Homo sapiens genus and its supposed evolutionary ancestors:

For references for the numbers given here see the Appendix 1.

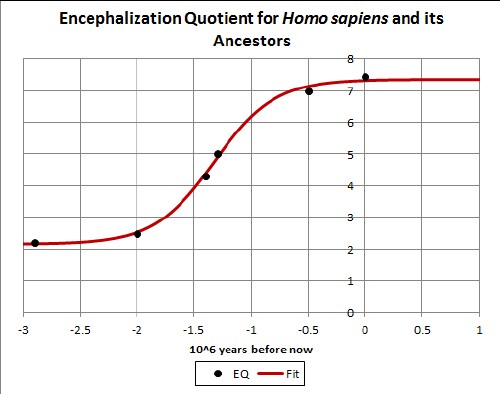
It appears from the numbers that EQ has transitioned from a low value to a high one. So, I shall fit the hyperbolic-tangent function to the data, since it is a mathematical way to represent such a transition.

Fit to the Data

See Appendix 2 for the fitting procedure.

The parameters of the fit are:

The following show the fit curve and the data fitted:

Conclusion

The encephalization quotient for the genus Homo appears to have transitioned from an original value of ~2.2 to a final value of ~7.4, indicating that intelligence for the Homo genus perhaps has reached its physical limit.

This work predicts EQ values for intermediate species between Australopithecus africanus and Homo habilis and between Homo erectus and Archaic Homo sapiens.

Appendix 1: References

• http://en.wikipedia.org/wiki/Encephalization_quotient
• http://www.aquaticape.org/eq.html
• http://members.cox.net/bvv/Evol-14.pdf
• http://www.psychomedia.it/pm/science/psybyo/mancia.htm
• http://www.coconutstudio.com/Brain%20Development.htm
• http://en.wikipedia.org/wiki/Australopithecus_afarensis
• http://en.wikipedia.org/wiki/Australopithecus_africanus
• http://en.wikipedia.org/wiki/Homo_habilis
• http://en.wikipedia.org/wiki/Homo_erectus
• http://en.wikipedia.org/wiki/Archaic_Homo_sapiens
• http://en.wikipedia.org/wiki/Homo_sapiens
• http://en.wikipedia.org/wiki/Homo_heidelbergensis
• http://en.wikipedia.org/wiki/Homo_rhodesiensis
• http://en.wikipedia.org/wiki/Homo_antecessor
• http://en.wikipedia.org/wiki/Homo_neanderthalensis

Appendix 2. Fitting Procedure

I fit the following hyperbolic-tangent function to the data:

,

where a = initial steady value, b = final steady value, t₀ is the "break" point (i.e., the place where the slope changes from increasing to decreasing) and w is the "width" or time constant when t represents time, as is the case here. The hyperbolic-time constant is twice the exponential time constant near the break point. Usually a = 0.

This function assumes that the data being fitted goes from one steady value, a, through a transition with break point, t₀, to a final steady value, b.

Silicon Intelligence Evolution
L. David Roper interdisciplinary studies

L. David Roper, http://www.roperld.com/personal/roperldavid.htm
6 April, 2016