Correlation Studies of Academic Excellence and Big‑Time Athletics
(A corrected version of an article published in
International Review of Sport Sociology, 3(11), Warsaw, Poland 1976, pp.57-69.)
L. David Roper (roperld@vt.edu) and Keith Snow (U.S.A.)
Abstract
Given particular measures of undergraduate excellence (U), graduate-school excellence (G), football excellence (F) and basketball excellence (B), we rank American universities in all four categories. Then the six correlation coefficients for all six pairs of the four categories are calculated: CUG=+0.033±0.053, CUF= –0.418±0.046, CUB= –0.496±0.033, CGF= –0.540±0.032, CGB= –0.556±0.038, CFB= –0.453±0.030. Several criticisms of our study and suggestions for future studies are made. Caution is particularly given that CUG may be considerably higher than the number we obtain.
I. Introduction
One occasionally hears the following justifications for the massive financial and sociological resources that are expended by universities and colleges for big‑time (i.e., highly visible) athletics:
(1) It attracts good students to the school, directly and indirectly.
(2) It attracts financial contributions (private and public) which enable programs of academic excellence.
It is interesting to consider whether these are the real reasons for big‑time athletics being in institutions of higher education, or whether there are other reasons along with or instead of these reasons.
To the author’s knowledge no systematic study of the veracity of these justifications has been published. The study reported here is a first attempt to do so. There are many faults with the approach adopted here. which we shall discuss later. Nevertheless, we believe that our results are valid, and we encourage others to refine or expand on our methods. Indeed, we offer aid to those who wish to do so.
In the next section we define “big‑time athletics” and specify our measure of it. In Section III we indicate our measures of graduate and undergraduate academic excellence. Section IV contains the mathematical definition of the correlation coefficient; this section may be skipped by readers who are not mathematically inclined. Finally, Section V gives our conclusions, some criticism of our approach and suggestions for further work.
II. Big Time Athletics
We define “big‑time” college and university
athletics to be varsity sports that receive the major attention of the news
media. Occasional casual glances at newspapers will convince one that men’s
football (American, not soccer) and basketball are by far the front runners.
Therefore, we further restrict our definition of big‑time athletics to
men’s football and basketball. Table 1 lists the Associated Press Polls and the
major bowl games and tournaments winners for football and basketball for the
years 1968 through 1972. From Table 1 we calculate the “score” listed in Table
2 by moving an entry up one rank when it won a major bowl game or tournament
and then adding the ranks for all five years for that entry and dividing by
five. (A team that was ranked in one or more years but was unranked in another
year was optimistically assumed to be in the twenty-first rank in the unranked
year.) An unranked entry that won a bowl game or tournament was assumed to be
ranked twentieth for that year. The football and basketball rankings given in
Tables 2 and 5 were then obtained by ordering the entries according to
decreasing score as given in Table 2.
|
Table 1 |
||||
|
Associated Press Polls and Major Bowl Game and
Tournament Winners |
||||
|
FOOTBALL |
||||
|
1968 |
1969 |
1970 |
1971 |
1972 |
|
1.
Ohio State |
1.
Texas |
1.
Nebraska |
1.
Nebraska |
1.
Southern California |
|
2.
Penn. State |
2.
Pennsylvania State |
2.
Notre Dame |
2.
Oklahoma |
2.
Oklahoma |
|
3.
Texas |
3.
Southern California |
3.
Texas |
3.
Colorado |
3.
Texas |
|
4.
Southern California |
4.
Ohio State |
4.
Tennessee |
4.
Alabama |
4.
Nebraska |
|
5.
Notre Dame |
5.
Notre Dame |
5.
Ohio State |
5.
Pennsylvania State |
5.
Auburn |
|
6.
Arkansas |
6.
Missouri |
6.
Arizona State |
6.
Michigan |
6.
Michigan |
|
7.
Kansas |
7.
Arkansas |
7.
Louisiana State |
7.
Georgia |
7.
Alabama |
|
8.
Georgia |
8.
Mississippi |
8.
Stanford |
8.
Arizona State |
8.
Tennessee |
|
9.
Missouri |
9.
Michigan |
9.
Michigan |
9.
Tennessee |
9.
Ohio State |
|
10.
Purdue |
10.
Louisiana State |
10.
Auburn |
10.
Stanford |
10.
Pennsylvania State |
|
11.
Oklahoma |
11.
Nebraska |
11.
Arkansas |
11.
Louisiana State |
11.
Louisiana State |
|
12.
Michigan |
12.
Houston |
12.
Toledo |
12.
Auburn |
12.
North Carolina |
|
13.
Tennessee |
13.
UCLA |
13.
Georgia Tech |
13.
Notre Dame |
13.
Arizona State |
|
14.
Southern Methodist |
14.
Florida |
14.
Dartmouth |
14.
Toledo |
14.
Notre Dame |
|
15.
Oregon State |
15.
Tennessee |
15.
Southern California |
15.
Mississippi |
15.
UCLA |
|
16.
Auburn |
16.
Colorado |
16.
Air Force |
16.
Arkansas |
16.
Colorado |
|
17.
Alabama |
17.
West Virginia |
17.
Tulane |
17.
Houston |
17.
North Carolina St. |
|
18.
Houston |
18.
Purdue |
18.
Pennsylvania State |
18.
Texas |
18.
Louisville |
|
19.
Louisiana State |
19.
Stanford |
19.
Houston |
19.
Washington (Seattle) |
19.
Washington State |
|
20.
Ohio |
20.
Auburn |
20.
Oklahoma (tie) |
20.
Southern California |
20.
Georgia Tech |
|
|
|
20.
Mississippi (tie) |
|
|
|
[Roanoke
Times Sat.
4 Jan. 1969] |
[Roanoke
Times Sun.
4 Jan. 1970] |
Roanoke
Times Wed.
6 Jan. 1971] |
[Roanoke
Times Tues.
4 Jan 1972] |
[Roanoke
Times Thurs.
4 Jan 1973] |
|
Bowl Winners: |
||||
|
Cotton-Texas |
Cotton-Texas |
Cotton-Notre
Dame |
Cotton-Pennsylvania
State |
Cotton-Texas |
|
Sugar-Arkansas |
Sugar-Mississippi |
Sugar-Tennessee |
Sugar-Oklahoma |
Sugar-Oklahoma |
|
Rose-Ohio
State |
Rose-Southern
California |
Rose-Stanford |
Rose-Stanford |
Rose-Southern
Calif. |
|
Orange-Pennsylvania
State |
Orange-Pennsylvania
State |
Orange-Nebraska |
Orange-Nebraska |
Orange-Nebraska
(forfeited) |
|
[Roanoke
Times Thurs.
2 Jan 1969] |
[Roanoke
Times Fri.
2 Jan 1970] |
[Roanoke
Times Sat.
2 Jan 1971] |
[Roanoke
Times Sun.
2 Jan 1942] |
[Roanoke
Times Tues.
2 Jan 1973] |
|
BASKETBALL |
||||
|
1968 |
1969 |
1970 |
1971 |
1972 |
|
1.
UCLA |
1.
Kentucky |
1.
UCLA |
1.
UCLA |
1.
UCLA |
|
2.
LaSalle |
2.
UCLA |
2.
Marquette |
2.
Pennsylvania |
2.
North Carolina St. |
|
3.
Santa Clara |
3.
St. Bonaventure |
3.
Pennsylvania |
3.
North Carolina |
3.
Minnesota |
|
4.
North Carolina |
4.
Jacksonville |
4.
Kansas |
4.
Louisville |
4.
Long Beach State |
|
5.
Davidson |
5.
New Mexico State |
5.Southern
California |
5.
Long Beach State |
5.
Providence |
|
6.
Purdue |
6.
South Carolina |
6.South
Carolina |
6.
South Carolina |
6.
Marquette |
|
7.
Kentucky |
7.
Iowa |
7.Western
Kentucky |
7.
Marquette |
7.
Houston |
|
8.
St. John’s, NY |
8.
Marquette |
8.
Kentucky |
8.
Brigham Young |
8.
North Carolina |
|
9.
Duquesne |
9.
Notre Dame |
9.
Fordham |
9.
Southwestern Louisiana |
9.
Indiana |
|
10.
Villanova |
10.
North Carolina State |
10.
Ohio State |
10.
Marshall |
10.
Maryland |
|
11.
Drake |
11.
Florida State |
11.Jacksonville |
11.
Memphis State |
11.
Kansas State |
|
12.
New Mexico State |
12.
Houston |
12.
Notre Dame |
12.
Hawaii |
12.
Missouri |
|
13.
South Carolina |
13.
Pennsylvania |
13.
North Carolina |
13.
Maryland |
13.
Syracuse |
|
14.
Marquette |
14.
Drake |
14.
Houston |
14.
Florida State |
14.
Southwestern Louisiana |
|
15.
Louisville |
15.
Davidson |
15.
Duquesne |
15.
Virginia |
15.
Memphis State |
|
16.
Boston College |
16.
Utah State |
16.
Long Beach State |
16.
Minnesota |
16.
Jacksonville |
|
17.
Notre Dame |
17.
Niagara |
17.
Tennessee |
17.
Oral Roberts |
17.
St. John’s, NY |
|
18.
Colorado |
18.
Western Kentucky |
18.
Villanova |
18.
Missouri |
18.
St. Joseph’s, PA |
|
19.
Kansas |
19.
Long Beach State |
19.
Drake |
19.
Houston |
19.
San Francisco State |
|
20.
Illinois |
20.
Southern California |
20.
Brigham Young |
20.
Indiana |
20.
Kentucky |
|
[Roanoke
Times Wed
5 Mar. 1969] |
[Roanoke
Times Wed
10 Mar. 1970] |
[Roanoke
Times Wed
16 Mar. 1971] |
[Roanoke
Times Wed
7 Mar. 1972] |
[Roanoke
Times Wed
7 Mar. 1973] |
|
Tournament Winners: |
||||
|
NCAA-UCLA |
NCAA-UCLA |
NCAA-UCLA |
NCAA-UCLA |
NCAA-UCLA |
|
NIT-Temple |
NIT-Marquette |
NIT-North
Carolina |
NIT-Maryland |
NIT-Virginia
Tech |
|
[Roanoke
Times Wed
23 Mar. 1969] |
[Roanoke
Times Wed
22 Mar. 1970] |
[Roanoke
Times Wed
28 Mar. 1971] |
[Roanoke
Times Wed
26 Mar. 1972] |
[Roanoke
Times Wed
26 & 27 Mar. 1973] |
|
Table 2 |
|||||
|
Football and Basketball Rankings |
|||||
|
Football |
Score |
Rank |
Basketball |
Score |
Rank |
|
Texas |
5.0 |
1 |
UCLA |
1.0 |
1 |
|
Pennsylvania
State |
6.8 |
2 |
Marquette |
7.2 |
2 |
|
Nebraska |
7.0 |
3 |
North
Carolina |
9.6 |
3 |
|
Notre
Dame |
7.6 |
4 |
South
Carolina |
10.4 |
4 |
|
Ohio
State |
7.8 |
.5 |
Kentucky |
11.2 |
5 |
|
Michigan |
8.4 |
6 |
Pennsylvania |
12.0 |
6 |
|
Tennessee |
9.6 |
7 |
Long
Beach State |
13.0 |
7 |
|
Oklahoma |
10.8 |
8 |
Jacksonville |
14.6 |
8.5 |
|
Louisiana
State |
11.6 |
9 |
Houston |
14.6 |
8.5 |
|
Arkansas |
12.0 |
10 |
North
Carolina State |
15.0 |
10 |
|
Southern
California |
12.2 |
11 |
Now
Mexico State |
16.0 |
11.5 |
|
Auburn |
12.6 |
12 |
Notre
Dame |
16.0 |
11.5 |
|
Arizona
State |
13.8 |
13 |
Louisville |
16.4 |
13.5 |
|
Alabama |
14.0 |
14 |
Minnesota |
16.4 |
13.5 |
|
Mississippi |
15.0 |
15 |
Davidson
|
16.6 |
15 |
|
Colorado |
15.4 |
16.5 |
Drake |
17.2 |
13 |
|
Stanford |
15.4 |
16.5 |
Kansas |
17.2 |
18 |
|
Georgia |
15.6 |
18 |
La
Salle |
17.2 |
18 |
|
Missouri |
16.8 |
19 |
Maryland |
17.2 |
18 |
|
Houston |
17.4 |
20 |
Southwestern
Louisiana |
17.2 |
18 |
|
Toledo |
17.8 |
21 |
Duquesne |
17.4 |
22 |
|
Kansas |
18.2 |
23 |
St.
Bonaventure |
17.4 |
22 |
|
Purdue |
18.2 |
23 |
Santa
Clara |
17.4 |
22 |
|
UCLA |
18.2 |
23 |
Florida
State |
17.6 |
25.5 |
|
North
Carolina |
19.2 |
25 |
St.
John’s, NY |
17.6 |
25.5 |
|
Georgia
Tech |
19.4 |
26 |
Southern
California |
17.6 |
25.5 |
|
Dartmouth |
19.6 |
28 |
Western
Kentucky |
17.6 |
25.5 |
|
Florida |
19.6 |
28 |
Memphis
State |
17.8 |
28.5 |
|
Southern
Methodist |
19.6 |
28 |
Providence |
17.8 |
28.5 |
|
Oregon
State |
19.8 |
30 |
Purdue |
18.0 |
30 |
|
Air
Force |
20.0 |
31 |
Brigham
Young |
18.2 |
32 |
|
North
Carolina State |
20.2 |
33 |
Iowa |
18.2 |
32 |
|
Tulane |
20.2 |
33 |
Villanova |
18.2 |
32 |
|
West
Virginia |
20.2 |
33 |
Indiana |
18.4 |
34 |
|
Louisville |
20.4 |
35 |
Fordharn |
18.6 |
35.5 |
|
Washington
(Seattle) |
20.6 |
36.5 |
Missouri |
18.6 |
35.5 |
|
Washington
State |
20.6 |
36.5 |
Marshall |
18.8 |
37.5 |
|
Ohio |
21.0 |
38 |
Ohio
State |
18.8 |
37.5 |
|
|
|
5 ties |
Kansas
State |
19.0 |
39 |
|
|
|
|
Hawaii |
19.2 |
40 |
|
|
|
|
Syracuse |
19.4 |
41 |
|
|
|
|
Virginia |
19.8 |
42 |
|
|
|
|
Boston
College |
20.0 |
43.5 |
|
|
|
|
Utah
State |
20.0 |
43.5 |
|
|
|
|
Oral
Roberts |
20.2 |
46 |
|
|
|
|
Niagara |
20.2 |
46 |
|
|
|
|
Tennessee |
20.2 |
46 |
|
|
|
|
Colorado |
20.4 |
48.5 |
|
|
|
|
St.
Joseph's, PA |
20.4 |
48.5 |
|
|
|
|
San
Francisco State |
20.6 |
50 |
|
|
|
|
Illinois |
20.8 |
52 |
|
|
|
|
Temple |
20.8 |
52 |
|
|
|
|
Virginia
Tech |
20.8 |
52 |
|
|
|
|
|
|
14 ties |
III. Academic Excellence
There are many methods one could use for measuring academic excellence. We make no attempt in this first effort to be exhaustive. In fact, we restrict ourselves to one measure of graduate-school excellence and one measure of undergraduate excellence.
1. Graduate School Excellence
For a graduate-school excellence measure we use the “effectiveness of graduate programs” ranking given by Roose and Andersen[1]. Scores for the entries in a field category were obtained by adding ranks for an entry that was ranked in at least one‑half of the curricula in a field category and dividing by the number of ranked curricula. The rankings in the five field categories listed in Table 3 were obtained by ranking these scores. Then a total score, also given in Table 3, was obtained for those entries ranked in three or more categories by adding the ranks and dividing by the number of ranked categories. For those ranked in only one or two categories, a score was obtained as indicated in the footnotes of Table 3. The final graduate school ranking, obtained by ordering the entries according to decreasing score, is listed in Tables 3 and 5.
|
Table 3 |
||||||||
|
“Effectiveness of Graduate Program” Ranking Obtained
from the Roose-Andersen Report and Graduate School Ranking |
||||||||
|
Program |
Humanities |
Soc. Sci. |
Bio. Sci. |
Phys. Sci. |
Engin. |
Score |
Footnotes |
Rank |
|
Harvard |
1 |
1 |
2 |
1 |
|
1.25 |
|
1 |
|
Calif.
(Berkeley) |
4 |
5 |
1 |
4 |
1 |
3.0 |
|
2 |
|
Calif.
Inst. Tech. |
|
|
4 |
2 |
4 |
3.3 |
|
3 |
|
Stanford |
6 |
7 |
3 |
3 |
1 |
4.0 |
|
4 |
|
Mass.
Inst. Tech. |
|
|
7 |
6 |
1 |
4.7 |
|
5 |
|
Princeton |
2 |
6 |
13 |
4 |
7 |
6.4 |
|
6 |
|
Wisconsin |
5 |
8 |
6 |
7 |
|
6.5 |
|
7 |
|
Yale |
3 |
3 |
11 |
12 |
|
7.25 |
|
8 |
|
Michigan |
8 |
2 |
8 |
14 |
6 |
7.6 |
|
9 |
|
Texas |
7 |
|
|
13 |
12 |
10.7 |
|
10 |
|
Chicago |
9 |
4 |
21 |
9 |
|
10.75 |
|
11 |
|
Cornell |
11 |
14 |
12 |
8 |
10 |
11.0 |
|
12 |
|
Illinois |
13 |
16 |
14 |
10 |
5 |
11.6 |
|
13 |
|
UCLA |
12 |
12 |
16 |
11 |
|
12.75 |
|
14 |
|
Rockefeller |
|
|
4 |
|
|
13.3 |
*3 |
15 |
|
Minnesota |
|
10 |
19 |
17 |
8 |
13.5 |
|
16 |
|
Johns
Hopkins |
14 |
17 |
10 |
|
|
13.7 |
|
17 |
|
Pennsylvania |
10 |
9 |
|
|
|
14.3 |
*1 |
18 |
|
Columbia |
15 |
13 |
|
16 |
|
14.7 |
|
19.5 |
|
Purdue |
|
|
17 |
|
9 |
14.7 |
*2 |
19.5 |
|
Wash.
(Seattle) |
|
|
9 |
|
|
15.0 |
*3 |
21 |
|
Indiana |
|
15 |
17 |
|
|
16.7 |
*2 |
22 |
|
Calif.
(Davis) |
|
|
15 |
|
|
17.0 |
*3 |
23 |
|
Carnegie
Mellon |
|
30 |
|
|
11 |
17.7 |
*4 |
24.5 |
|
Northwestern |
|
11 |
|
|
|
17.7 |
*4 |
24.5 |
|
Mich.
State |
|
|
20 |
|
|
18.7 |
*3 |
26 |
|
Calif.
(San Diego) |
|
|
|
15 |
|
19.0 |
*4 |
27 |
|
Brown |
16 |
|
|
|
|
19.3 |
*4 |
29 |
|
Case
Western Res. |
|
|
22 |
|
|
19.3 |
*3 |
29 |
|
Wash.
(St. Louis) |
|
|
22 |
|
|
19.3 |
*3 |
29 |
|
|
|
|
|
|
|
|
|
3 ties |
|
Footnotes:
*1: Added 24 & ÷3; *2: Added 18
& ÷3; *3: Added (18+18) & ÷3; *4: Added (24+18) & ÷3 |
||||||||
Undergraduate Excellence
Since often the justification for involving educational institutions with big‑time athletics is that it attracts good students, we restrict ourselves to some measure of the academic excellence of the students attracted to an institution; i.e., incoming freshmen. Because the SAT scores of entering freshmen are available in Singletary's[2] compendium, we use the average SAT score (average of verbal and mathematical scores) as a ranking measure.
Table 4 lists the average SAT score for a selection of schools. The Singletary compendium does not give SAT scores for some schools. Our selection includes all those available in Singletary that are ranked in Tables 2 and 3 and most colleges and universities with average SAT scores higher than 599. (We say “most” because we did not attempt to find all such schools.) By excluding schools which are both unranked in Tables 2 and 3 and have SAT scores below 600 we bias our results toward larger correlations between undergraduate quality and the other qualities. Similarly, by not systematically searching for all schools unranked in Tables 2 and 3 with average SAT scores higher than 599, we again bias toward larger correlations.
|
Table 4 |
||||||||
|
Undergraduate Freshmen
Average SAT Score Ranking |
||||||||
|
|
SAT |
Rank |
|
SAT |
Rank |
|
SAT |
Rank |
|
Calif. Inst. Tech. |
715 |
1 |
Washington (St. Louis) |
611 |
40 |
North Carolina State |
536 |
79 |
|
Mass. Inst. Tech. |
714 |
2 |
Stevens Inst. Tech. |
610 |
41 |
Delaware |
535 |
81 |
|
Harvard |
695 |
3 |
Carnegie Mellon |
609 |
42.5 |
La Salle |
535 |
81 |
|
Yale |
690 |
4 |
Case West. Res. |
609 |
42.5 |
Vermont |
535 |
81 |
|
Rice |
684 |
5 |
SUNY (Stoney Brook) |
607 |
44 |
Southern Methodist |
534 |
83 |
|
Brandeis |
669 |
6 |
William & Mary |
606 |
45 |
Providence |
530 |
84 |
|
Brown |
665 |
8 |
Northwestern |
604 |
46.5 |
St. Bonaventure |
523 |
85 |
|
Chicago |
665 |
8 |
Wabash |
604 |
46.5 |
Auburn |
522 |
86 |
|
Reed |
665 |
8 |
Boston U. |
600 |
48.5 |
Mass. (Boston) |
520 |
87 |
|
Carleton |
662 |
11 |
Michigan |
600 |
48.5 |
Cincinnati |
517 |
89 |
|
Dartmouth |
662 |
11 |
SUNY (Buffalo) |
595 |
50 |
Detroit |
517 |
89 |
|
Williams |
662 |
11 |
Georgia Tech. |
593 |
51 |
Texas A&M |
517 |
89 |
|
Columbia |
661 |
13.5 |
New York |
589 |
52 |
San Francisco State |
516 |
91.5 |
|
Princeton |
661 |
13.5 |
George Washington |
587 |
53 |
St. John's, NY |
516 |
91.5 |
|
Oberlin |
660 |
15 |
Syracuse |
583 |
54 |
Niagara |
515 |
93 |
|
Cornell |
657 |
16 |
Tulane |
582 |
55 |
South Florida |
514 |
94 |
|
Pennsylvania |
655 |
17 |
St. Joseph's, Pa. |
579 |
56 |
Toledo |
513 |
95 |
|
Middlebury |
650 |
18 |
CCNY |
577 |
58 |
Louisville |
512 |
97.5 |
|
Renss. Poly. Inst. |
648 |
19 |
Massachusetts (Amherst) |
577 |
58 |
Ohio |
512 |
97.5 |
|
Johns Hopkins |
646 |
20 |
Wisconsin |
577 |
58 |
Oregon |
512 |
97.5 |
|
Rochester |
645 |
21 |
North Carolina |
576 |
60 |
Tulsa |
512 |
97 |
|
Air Force |
640 |
23 |
Miami (Ohio) |
575 |
61 |
Texas Christian |
511 |
100.5 |
|
Davidson |
640 |
23 |
Wake Forest |
572 |
62 |
Wayne State |
511 |
100.5 |
|
Lehigh |
640 |
23 |
Pennsylvania State |
570 |
63 |
Georgia |
510 |
102 |
|
Tufts |
635 |
25 |
Santa Clara |
569 |
64 |
Missouri |
509 |
103 |
|
Duke |
629 |
26 |
Pittsburgh |
562 |
65 |
Rhode Island |
507 |
104 |
|
Georgetown |
628 |
27.5 |
Northeastern |
558 |
66.5 |
Indiana |
505 |
105 |
|
Grinnell |
628 |
27.5 |
Rutgers |
558 |
66.5 |
Houston |
504 |
106 |
|
Boston College |
627 |
29.5 |
Maine |
557 |
68 |
Arkansas |
503 |
107.5 |
|
Colgate |
627 |
29.5 |
Virginia Mil. Inst. |
553 |
69 |
Duquesne |
503 |
107.5 |
|
Antioch |
626 |
31.5 |
Virginia Tech. |
551 |
70 |
Temple |
502 |
109 |
|
Vanderbilt |
626 |
31.5 |
Connecticut |
550 |
72 |
Oregon State |
500 |
110 |
|
Naval Academy |
621 |
33 |
Fairfield |
550 |
72 |
South Carolina |
498 |
111 |
|
Virginia |
618 |
34.5 |
Villanova |
550 |
72 |
Arizona |
496 |
112 |
|
West Point |
618 |
34.5 |
Texas (Austin) |
547 |
74 |
Hawaii |
495 |
113 |
|
SUNY (Bingh.) |
615 |
36 |
Miami (Florida) |
546 |
75 |
Idaho |
483 |
114 |
|
Fordham |
613 |
37 |
Southern California |
544 |
76 |
Jacksonville |
471 |
115 |
|
Emory |
612 |
38.5 |
New Hampshire |
543 |
77.5 |
Texas Tech |
468 |
116 |
|
Washington & Lee |
612 |
38.5 |
Purdue |
543 |
77.5 |
22 ties |
|
|
|
Table 5 |
|||||||||
|
Collection of All Rankings |
|||||||||
|
School |
Undergrad. |
Graduate |
Football |
Basketball |
School |
Undergrad. |
Graduate |
Football |
Basketball |
|
Calif.
I. Tech |
1 |
3 |
|
|
Wisconsin |
57 |
7 |
|
|
|
Mass.
I. Tech |
2 |
5 |
|
|
North
Carolina |
60 |
|
25 |
3 |
|
Harvard |
3 |
1 |
|
|
Miami
(Ohio) |
61 |
|
|
|
|
Yale |
4 |
8 |
|
|
Wake
Forest |
62 |
|
|
|
|
Rice |
5 |
|
|
|
Penn.
State |
63 |
|
2 |
|
|
Brandeis |
6 |
|
|
|
Santa
Clara |
64 |
|
|
21 |
|
Brown |
7 |
28 |
|
|
Pittsburgh |
65 |
|
|
|
|
Chicago |
7 |
11 |
|
|
Northeastern |
66 |
|
|
|
|
Reed |
7 |
|
|
|
Rutgers |
66 |
|
|
|
|
Carleton |
10 |
|
|
|
Maine |
68 |
|
|
|
|
Dartmouth |
10 |
|
27 |
|
Va.
Mil. Inst. |
69 |
|
|
|
|
Williams |
10 |
|
|
|
Virginia
Tech |
70 |
|
|
51 |
|
Columbia |
13 |
19 |
|
|
Connecticut |
71 |
|
|
|
|
Princeton |
13 |
6 |
|
|
Fairfield |
71 |
|
|
|
|
Oberlin |
15 |
|
|
|
Villanova |
71 |
|
|
31 |
|
Cornell |
16 |
12 |
|
|
Texas
(Austin) |
74 |
10 |
1 |
|
|
Pennsylvania |
17 |
18 |
|
6 |
Miami
(Fl.) |
75 |
|
|
|
|
Middlebury |
18 |
|
|
|
Southern
Calif. |
76 |
|
11 |
24 |
|
Renss.
Poly. Inst. |
19 |
|
|
|
New
Hampshire |
77 |
|
|
|
|
Johns
Hopkins |
20 |
17 |
|
|
Purdue |
77 |
19 |
23 |
30 |
|
Rochester |
21 |
|
|
|
N.
Carolina St. |
79 |
|
32 |
10 |
|
Air
Force |
22 |
|
31 |
|
Delaware |
80 |
|
|
|
|
Davidson |
22 |
|
|
15 |
La
Salle |
80 |
|
|
16 |
|
Lehigh |
22 |
|
|
|
Vermont |
80 |
|
|
|
|
Tufts |
25 |
|
|
|
Southern
Meth. |
83 |
|
27 |
|
|
Duke |
26 |
|
|
|
Providence |
84 |
|
|
28 |
|
Georgetown |
27 |
|
|
|
St.
Bonaventure |
85 |
|
|
21 |
|
Grinnell |
27 |
|
|
|
Auburn |
86 |
|
12 |
|
|
Colgate |
29 |
|
|
|
Mass.
(Boston) |
87 |
|
|
|
|
Boston
College |
29 |
|
|
|
Cincinnati |
88 |
|
|
|
|
Antioch |
31 |
|
|
|
Detroit |
88 |
|
|
|
|
Vanderbilt |
31 |
|
|
|
Texas
A & M |
88 |
|
|
|
|
Naval
Acad. |
33 |
|
|
|
St.
John’s, NY |
91 |
|
|
24 |
|
Virginia |
34 |
|
|
42 |
San.
Fran. State |
91 |
|
|
50 |
|
West
Point |
34 |
|
|
|
Niagara |
93 |
|
|
45 |
|
SUNY
(Binghamton) |
36 |
|
|
|
South
Florida |
94 |
|
|
|
|
Fordham |
37 |
|
|
35 |
Toledo |
95 |
|
21 |
|
|
Emory |
38 |
|
|
|
Louisville |
96 |
|
35 |
13 |
|
Wash.
& Lee |
38 |
|
|
|
Ohio |
96 |
|
38 |
|
|
Wash.
(St. Louis) |
40 |
28 |
|
|
Oregon |
96 |
|
|
|
|
Stevens
I. Tech |
41 |
|
|
|
Tulsa |
96 |
|
|
|
|
Carnegie
Mellon |
42 |
24 |
|
|
Texas
Christian |
100 |
|
|
|
|
Case
West. Res. |
42 |
28 |
|
|
Wayne
State |
100 |
|
|
|
|
SUNY
(Stoney Br.) |
44 |
|
|
|
Georgia |
102 |
|
18 |
|
|
William
& Mary |
45 |
|
|
|
Missouri |
103 |
|
19 |
35 |
|
Northwestern |
46 |
24 |
|
|
Rhode
Island |
104 |
|
|
|
|
Wabash |
46 |
|
|
|
Indiana |
105 |
22 |
|
34 |
|
Boston
University |
48 |
|
|
|
Houston |
106 |
|
20 |
8 |
|
Michigan |
48 |
9 |
6 |
|
Arkansas |
107 |
|
10 |
|
|
SUNY
(Buffalo) |
50 |
|
|
|
Duquesne |
107 |
|
|
21 |
|
Georgia
Tech. |
51 |
|
26 |
|
Temple |
109 |
|
|
51 |
|
New
York |
52 |
|
|
|
Oregon
State |
110 |
|
30 |
|
|
George
Washington |
53 |
|
|
|
South
Carolina |
111 |
|
|
4 |
|
Syracuse |
54 |
|
|
41 |
Arizona |
112 |
|
|
|
|
Tulane |
55 |
|
32 |
|
Hawaii |
113 |
|
|
40 |
|
St.
Joseph’s, PA |
56 |
|
|
48 |
Idaho |
114 |
|
|
|
|
CCNY |
57 |
|
|
|
Jacksonville |
115 |
|
|
8 |
|
Mass.
(Amherst) |
57 |
|
|
|
Texas
Tech. |
116 |
|
|
|
|
Table 5 (continued) |
||||||||||||
|
Collection of All Rankings |
||||||||||||
|
School |
Undergrad. |
Graduate |
Football |
Basketball |
School |
Undergrad. |
Graduate |
Football |
Basketball |
|||
|
Alabama |
|
|
14 |
|
Memphis
State |
|
|
|
28 |
|||
|
Arizona
State |
|
|
13 |
|
Michigan
State |
|
26 |
|
|
|||
|
Brigham
Young |
|
|
|
31 |
Minnesota |
|
16 |
|
13 |
|||
|
California
(Berkeley) |
|
2 |
|
|
Mississippi |
|
|
15 |
|
|||
|
California
(Davis) |
|
23 |
|
|
Nebraska |
|
|
3 |
|
|||
|
UCLA |
|
14 |
22 |
1 |
New
Mexico St. |
|
|
|
11 |
|||
|
California
(San Diego) |
|
27 |
|
|
Notre
Dame |
|
|
4 |
11 |
|||
|
Colorado |
|
|
16 |
48 |
Ohio
State |
|
|
5 |
37 |
|||
|
Drake |
|
|
|
16 |
Oklahoma |
|
|
8 |
|
|||
|
Florida |
|
|
27 |
24 |
Oral
Roberts |
|
|
|
45 |
|||
|
Illinois |
|
13 |
|
51 |
Rockefeller |
|
15 |
|
|
|||
|
Iowa |
|
|
|
31 |
Southwestern
La. |
|
|
|
16 |
|||
|
Kansas |
|
|
|
16 |
Stanford |
|
4 |
16 |
|
|||
|
Kansas
State |
|
|
24 |
39 |
Tennessee |
|
|
7 |
45 |
|||
|
Kentucky |
|
|
|
5 |
Utah
State |
|
|
|
43 |
|||
|
Long
Beach State |
|
|
|
7 |
Wash.
(Seattle) |
|
21 |
36 |
|
|||
|
Louisiana
State |
|
|
9 |
|
Washington
State |
|
|
36 |
|
|||
|
Marquette |
|
|
|
2 |
Western
Kentucky |
|
|
|
24 |
|||
|
Marshall |
|
|
|
37 |
West
Virginia |
|
|
32 |
|
|||
|
Maryland |
|
|
|
16 |
|
|
|
|
|
|||
|
|
|
|
|
|
Numbers
ranked: |
116 |
30 |
38 |
51 |
|||
|
|
|
|
|
|
Number
of ties: |
22 |
3 |
5 |
14 |
|||
IV. CORRELATION COEFFICIENT
We use the expression for the correlation coefficient for two different rankings derived in the book by Yule and Kendall[3]. This expression allows for the possibility of tied ranks. It is
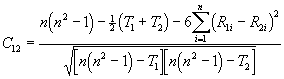
where 
is the total number
of entries, 
is the rank of the ith entry in the first ranking; 
is the rank of the ith entry in the second ranking;
,
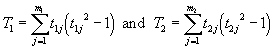where 
is the number of ties
in the first ranking, 
is the number of ties
in the second ranking and 
is the number that
are tied in the jth tie for
the ranking in question. The 
for tied ranks are
the average ranking for the particular tie in question; i.e., if 
entries occupy the
ranks 
then
.
These values of 
are listed for the
tied entries in Tables 2, 3 and 4.
But we have a further
complication not discussed by Yule and Kendall; namely, we have entries that
are ranked in only one of the two rankings to be compared. We handle this
situation as follows: Let 
be the total number
of different entries in both rankings (as given above), 
be the number of
entries in the first ranking and 
be the number of
entries in the second ranking. Thus, there are 
entries that are
unranked in the first ranking and 
entries that are
unranked in the second ranking. We use a computer random generator to randomly
fill all of the ranks from 
to 
for the first ranking
and from 
to 
for the second
ranking. Since surely some of these entries should be truly ranked larger than 
, this procedure should favor larger correlations.
We do this residual random ranking a large number of times (1000 times) and take the average correlation coefficient and the standard deviation as our correlation coefficient and its error. The results are listed in Table 6.
|
Table 6 |
||||
|
Average Correlation Coefficients and Standard
Deviations |
||||
|
Undergraduate |
1. |
|
|
|
|
Graduate |
+0.033±0.053 |
1. |
|
|
|
Football |
-0.418±0.046 |
-0.540±0.032 |
1. |
|
|
Basketball |
-0.496±0.033 |
-0.556±0.038 |
-0.453±0.030 |
1. |
|
|
Undergraduate |
Graduate |
Football |
Basketball |
|
Maximum and Minimum
Correlation Coefficients Obtained in 1000 Residual Random Rankings |
||||
|
Undergraduate |
1 |
|
|
|
|
Graduate |
+0.192 -0.125 |
1 |
|
|
|
Football |
-0.275 -0.580 |
-0.433 -0.635 |
1 |
|
|
Basketball |
-0.382 -0.591 |
-0.441 -0.669 |
-0.354 -0.541 |
1 |
|
|
Undergraduate |
Graduate |
Football |
Basketball |
V. Conclusion and Criticism
Before discussing the results in Table 6, perhaps we should state what correlation coefficients indicate. A correlation coefficient of +1 for two rankings indicates that the two rankings are identical. A correlation coefficient of -1 indicates that the two rankings are exactly opposite. A coefficient of 0 would indicate that the two rankings are totally random relative to each other. Thus, a large positive correlation coefficient indicates that the two rankings closely coincide and a large negative coefficient indicates that the two rankings are nearly anti-coincident.
Table 6 clearly shows that, for the methods of ranking that we use, there are significant negative correlations between all pairs of ranking except undergraduate versus graduate. In this one exceptional comparison the correlation is effectively zero, although it should be pointed out that this correlation may be greater than zero for large schools and that we were not able to obtain freshman SAT scores for several highly ranked graduate schools that we suspect have high freshman SAT scores. A more careful study should be done on this correlation; it is not our main purpose here.
So it appears that the contentions that big‑time athletics (1) attracts good students and (2) enables programs of academic excellence are both false. It also appears that concentration on excellence in one big‑time sport usually excludes excellence in the other big‑time sport. However, concentration on excellence in either graduate or undergraduate education does not exclude excellence in the other. Have we possibly biased the result toward small correlations? As indicated above, at various stages, we have always tried to bias it toward large correlations when there was a choice.
1. Other methods of ranking could be used. For example, percentage of students who go on to graduate school could be used as a measure of undergraduate excellence. This would measure the product of the school rather than the “raw material” measure that we used.
2. We did not study rankings of small colleges with regard to athletic excellence. We believe that most of the small colleges with strong big-time athletic programs are ranked quite low on average SAT scores for incoming freshmen. If so, then our results stand. Further study is needed on this point.
3. Singletary's compendium2 did not give entering SAT scores for some schools that we know must be truly highly ranked according to SAT scores. We suspect that this correction would lower the correlation coefficients. Further study is desirable.
4. A further study should separate out schools of different student body sizes to see if large schools are able to simultaneously promote athletics and academic excellence more easily than can small schools.
5. A further study should separate out state‑supported schools from private schools to see if there are differences between the two types.
6. An interesting question to pursue is: Is the United States the only country where big‑time sports and education institutions are intimately connected?
If our conclusions remain after further study, one must ask the question: What is the actual connection between big‑time sports and educational institutions? We would offer an hypothesis: Societies from the “beginning” have depended upon physical prowess for their survival, and, thus, have come to savor physical combat; and the most likely combatants are young men. Now that societies are “suddenly” depending more on intellectual capacity, which must be constantly developed from an early age, it is understandable why these seemingly unrelated emphases are found together in institutions for development of the young.
But our newly acquired intellectual capacity compels us to ask: Is that the best way? Should we, instead, have separate institutions dedicated to these unrelated pursuits? Of course, we do have professional sports organizations and we have many educational institutions (our best, as this study shows) that do not emphasize big‑time sports. Would not our society better recognize its increasing dependence on intellectual capability over physical prowess if the institutions that promote the two were separate and distinct? And would not institutions supposedly dedicated to increasing our intellectual capability be better able to use their limited financial and sociological resources to that end if they were not diverted to the unrelated pursuit of physical prowess?
We want to make it clear that we believe that assurance of physical fitness for all students is a necessary part of any educational program. We would urge an expansion of athletic programs for all students coincident with curtailment of big-time athletics in our institutions of higher education.
One of the authors (LDR) would be glad to run the computer code used here on any reasonable set of measures for academic excellence ranking.
The authors wish to thank Mr. Michael Tarpley, Dr. Robert L. Shotwell, Dr. Richard A. Arndt and several other colleagues, who may wish that their names not be mentioned, for help they have given us.